Hata Model for Urban Areas

In wireless communication, the Hata Model for Urban Areas, also known as the Okumura-Hata model for being a developed version of the Okumura Model, is the most widely used radio frequency propagation model for predicting the behaviour of cellular transmissions in built up areas. This model incorporates the graphical information from Okumura model and develops it further to realize the effects of diffraction, reflection and scattering caused by city structures. This model also has two more varieties for transmission in Suburban Areas and Open Areas.[1]

Hata Model predicts the total path loss along a link of terrestrial microwave or other type of cellular communications.

Contents

Applicable to/under conditions

This particular version of the Hata model is applicable to the radio propagation within urban areas.

This model is suited for both point-to-point and broadcast transmissions and it is based on extensive empirical measurements taken.

PCS is another extension of the Hata model. The Walfisch and Bertoni Model is further advanced.

Coverage

Frequency: 150 MHz to 1500 MHz

Mobile Station Antenna Height: between 1 m and 10 m

Base station Antenna Height: between 30 m and 200 m

Link distance: between 1 km and 20 km.

Mathematical formulation

Hata Model for Urban Areas is formulated as:

L_U \; = \; 69.55 \; %2B \; 26.16 \; \log f \; - \; 13.82 \; \log h_B \; - \; C_H \; %2B \; [44.9 \; - \; 6.55 \; \log h_B] \; \log d

For small or medium sized city,

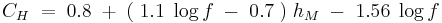
C_H \; = \; 0.8 \; %2B \; (\; 1.1 \; \log f \; - \; 0.7 \; ) \; h_M \; - \; 1.56 \; \log f

and for large cities,

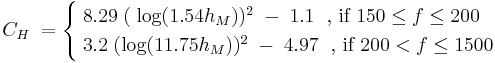
C_H \; = \begin{cases}\;8.29 \; (\; \log ({1.54 h_M}))^2 \; - \; 1.1 \; \mbox{ , if } 150 \le f \le 200 \\ \; 3.2 \; (\log ({11.75 h_M}))^2 \; - \; 4.97 \; \mbox{ , if }200 < f \le 1500 \end{cases}

Where,

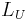L_U\; = Path loss in Urban Areas. Unit: decibel (dB)

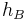h_B\; = Height of base station Antenna. Unit: meter (m)

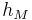h_M\; = Height of mobile station Antenna. Unit: meter (m)

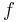f\; = Frequency of Transmission. Unit: megahertz(MHz).

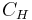C_H\; = Antenna height correction factor

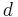d\; = Distance between the base and mobile stations. Unit: kilometer (km).

Points to note Walfisch and bertoni model

A model developed by Walfisch and Bertoni [Wa]88] considers the impact of rooftops and building height by using diffraction to predict average signal strength at street level. The model considers the path loss, S, to be a product of three factors. S = Po Q2 P1 where P0 represents free space path loss between isotropic antennas given by

Po = (lambda / 4 pai R)2 (whole square) The factor Q2 gives the reduction in the rooftop signal due to the row of buildings which immediately shadow the receiver at street level. The P1 term is based upon diffraction and determines the signal loss from the rooftop to the street. In dB, the path loss is given by S(dB) =Lo+Lrts+Lms

where L0 represents free space loss, Lrts represents the "rooftop-to-street diffraction and scatter loss", and Lms denotes multiscreen thffiaction loss due to the rows of buildings [X1a92]. This model is being considered for use by ITU-R in the IMT-2000 standards activities.

THIS PARAGRAPH IS FROM THE BOOK: Wireless Communications by Theodore S. Rappaport, p157, ch 4.11

Limitations

Though based on the Okumura Model, the Hata model does not provide coverage to the whole range of frequencies covered by Okumura Model. Hata model does not go beyond 1500 MHz while Okumura provides support for up to 1920 MHz.

References

  1. ^ Seybold, John S. (2005). Introduction to RF propagation. John Wiley and Sons. ISBN 0471655961. 

External links

See also